https://www.acmicpc.net/problem/16565

묘하게 재귀로 풀 수 있을 것 같았는데, 실패해서 다른 블로그 힌트를 보며 풀었다.
다들 '포함-배제의 원리'를 사용해서 풀고 있었다.
[조합론] 포함-배제의 원리(Inclusion-Exclusion Principle)
포함-배제의 원리란?포함-배제의 원리(Inclusion-Exclusion Principle)란 여러 집합들의 합집합의 크기를 구하는 데 사용하는 공식이다.포함-배제의 원리는 교집합의 크기로 합집합의 크기를 구하거나,
mango-juice.com
두 집합 $A, B$가 있을 때 $|A \cup B|$의 크기는 다음과 같다.
$$|A \cup B| = |A| + |B| - |A \cap B|$$
그리고 세 집합 $A, B, C$가 있을 때 $|A \cup B \cup C|$의 크기는 다음과 같다.
$$|A \cup B \cup C| = (|A| + |B| + |C|) - (|A \cap B| + |A \cap C| + |B \cap C|) + (|A \cap B \cap C|)$$
이처럼 홀수 개의 집합식은 더해주고, 짝수 개의 집합으로 이루어진 집합식은 빼주는 것을 볼 수 있다.
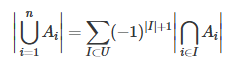
일반화하면 다음과 같은 식을 얻을 수 있다.
그리고 N포커의 문제는 포카드를 갖고 있는 경우의 수를 구해야 한다.
$N=13$일 때, 포카드의 경우는 다음과 같다.
- 1개의 포카드를 갖는 경우
- 2개의 포카드를 갖는 경우
- 3개의 포카드를 갖는 경우
1. 1개의 포카드를 갖는 경우
이 경우 아래의 식과 같이 생각할 수 있다.
$$f(1) = _{13}C_{1} \times _{52-4}C_{13-4}$$
이 때, 2개의 포카드를 가지는 경우와 3개의 포카드를 가지는 경우를 포함한다.
2. 2개의 포카드를 갖는 경우
$$f(2) = _{13}C_{2} \times _{52-8}C_{13-8}$$
이 때, 3개의 포카드를 가지는 경우를 포함한다.
3. 3개의 포카드를 갖는 경우
$$f(3) = _{13}C_{3} \times _{52-12}C_{13-12}$$
이를 위의 포함배제의 원리에 적용한다면,
$$f(1) - f(2) + f(3)$$
위의 방식으로 전체 포카드 경우의 수를 구할 수 있다.
# https://www.acmicpc.net/problem/16565
# 수학
import sys
import operator as op
from functools import reduce
N = int(input())
div = 10007
def combination(n, r) :
if n < 1 or r < 0 or n < r :
return 1
r = min(r, n - r)
numerator = reduce(op.mul, range(n, n-r, -1), 1)
denominator = reduce(op.mul, range(1, r+1), 1)
return numerator // denominator
ans = 0
if N >= 4 :
for i in range(1, N // 4 + 1) :
if i % 2 == 1 :
ans += combination(13, i) * combination(52 - 4*i, N - 4*i)
else :
ans -= combination(13, i) * combination(52 - 4*i, N - 4*i)
print(ans % div)
'코테풀이 > 백준' 카테고리의 다른 글
| 2839번: 설탕 배달 (0) | 2025.11.20 |
|---|---|
| 15824번: 너 봄에는 캡사이신이 맛있단다 (0) | 2025.11.02 |
| 1629번: 곱셈 (0) | 2025.10.27 |
| 13334번: 철로 (0) | 2025.10.18 |
| 2170번: 선 긋기 (0) | 2025.10.18 |