https://www.acmicpc.net/problem/1753
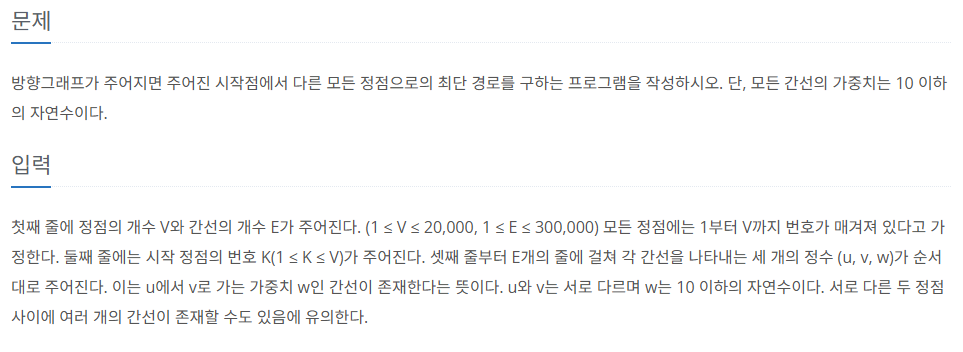
BFS로 자신있게 풀어봐야지! 했다가, 가중치가 주어져 있어서 다익스트라를 사용하기로 했다.
다익스트라의 경우, 음의 가중치가 있을 때 사용할 수 없다고 한다.
# https://www.acmicpc.net/problem/1753
# 다익스트라
import sys
import heapq
from collections import defaultdict
V, E = map(int, sys.stdin.readline().split()) # 정점 개수, 간선 개수
K = int(input()) # start
# graph
graph = defaultdict(list)
for _ in range(E) :
u, v, w = map(int, sys.stdin.readline().split())
graph[u].append((v, w))
def dijkstra(start, V) :
INF = 1e8
distance = [INF] * (V + 1)
q = []
heapq.heappush(q, (0, start)) # 우선순위, 값 형태로 입력
distance[start] = 0
while q :
dist, now = heapq.heappop(q) # 우선순위가 가장 낮은 값
if distance[now] < dist :
continue
for i in graph[now] :
if dist + i[1] < distance[i[0]] :
distance[i[0]] = dist + i[1]
heapq.heappush(q, (dist + i[1], i[0]))
for elem in distance[1:] :
if elem == INF :
print("INF")
else : print(elem)
dijkstra(K, V)
다익스트라(Dijkstra) 알고리즘
다익스트라(Dijkstra) 알고리즘은 그래프 이론을 활용한 대표적인 최단 경로(Shortest Path)탐색 알고리즘이다. 이 알고리즘은 특정한 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 구할 수
deulee.tistory.com
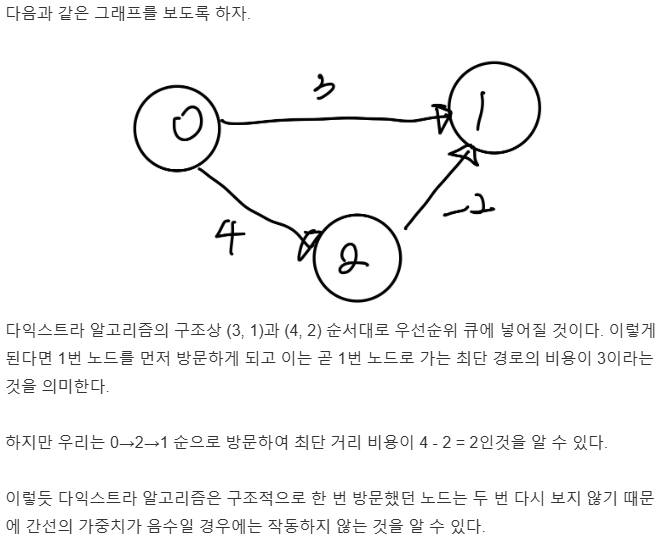
위 링크에서 가중치가 음수일 때 다익스트라를 사용할 수 없는 이유를 보여준다.
0->2->1로 가는 것이 가중치 합이 2로 작지만, 구조적으로 한 번 방문했던 노드를 다시 볼 수 없기 때문에 작동할 수 없다고 한다.
이럴 때 벨만 포드 알고리즘을 사용한다고 한다.
다익스트라 알고리즘 with python
다익스트라 알고리즘은 최단거리를 구하는 알고리즘입니다. 다익스트라 알고리즘을 사용하면, 하나의 노드에서 다른 모든 노드까지의 거리를 구할 수 있습니다. 개인적으로 개념을 이해하는
velog.io
위 블로그에서, 다익스트라 알고리즘을 heap을 사용하여 구현했다.
이를 참고하여 문제를 풀어보았다.
그래프 생성
# graph
graph = defaultdict(list)
for _ in range(E) :
u, v, w = map(int, sys.stdin.readline().split())
graph[u].append((v, w))그래프는 u에서 v로 가는 경우, 가중치 w를 함께 저장하도록 했다.
directional graph이므로, v에서 u로 가는 경우는 저장하지 않았다.
다익스트라
def dijkstra(start, V) :
INF = 1e8
distance = [INF] * (V + 1)
q = []
heapq.heappush(q, (0, start)) # 우선순위, 값 형태로 입력
distance[start] = 0
while q :
dist, now = heapq.heappop(q) # 우선순위가 가장 낮은 값
if distance[now] < dist :
continue
for i in graph[now] :
if dist + i[1] < distance[i[0]] :
distance[i[0]] = dist + i[1]
heapq.heappush(q, (dist + i[1], i[0]))
for elem in distance[1:] :
if elem == INF :
print("INF")
else : print(elem)distance 설정
INF값으로 1e8을 사용하고, 해당 값을 요소로 V+1개를 갖는 리스트 distance를 생성한다.
INF = 1e8
distance = [INF] * (V + 1)
heap큐와 distance[start] 초기화
q = []
heapq.heappush(q, (0, start)) # 우선순위, 값 형태로 입력
distance[start] = 0heap큐인 q에 가중치(우선순위)가 먼저 오도록 튜플 형태로 넣어주고,
자기 자신과의 거리인 distance[start]는 0으로 설정한다.
최단 거리 구하기
while q :
dist, now = heapq.heappop(q) # 우선순위가 가장 낮은 값
if distance[now] < dist : # 이미 방문한 경우
continue
for i in graph[now] :
if dist + i[1] < distance[i[0]] : # 기존 distance에 저장된 값이 더 크다면
distance[i[0]] = dist + i[1]
heapq.heappush(q, (dist + i[1], i[0]))heapq.heappop(q)를 사용하여 가장 가중치(거리, 우선순위)가 작은 노드를 얻는다. = dist, now
distance[now]의 값이 dist보다 작은 경우는 이미 방문한 노드이기 때문에 넘어간다.
그 후에, 그래프 탐색을 진행한다.
만약 지금까지의 거리와 앞으로 탐색할 노드의 거리의 합이 distance에 저장된 값보다 작다면,
distance에 거리의 합을 저장하고(방문 처리)
heapq인 q에 거리의 합과 정점을 함께 push한다.
정답 출력
for elem in distance[1:] :
if elem == INF :
print("INF")
else : print(elem)정점은 1부터 시작하기 때문에 slicing된 distance부터 차례로 출력한다.
elem의 값이 1e8인 경우, "INF"를 출력하도록 하고,
그렇지 않은 경우, 거리를 출력하도록 한다.
'코테풀이 > 백준' 카테고리의 다른 글
| 10026번: 적록색약 (1) | 2025.09.15 |
|---|---|
| 14502번: 연구소 (0) | 2025.09.13 |
| 1697번 : 숨바꼭질 (0) | 2025.09.09 |
| 7576: 토마토 (0) | 2025.09.08 |
| 1012번: 유기농 배추 (0) | 2025.09.08 |